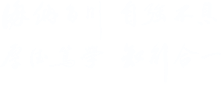报告题目: On the ⋆-congruence Sylvester equation

报告人：张绍良 教授（名古屋大学）

报告时间：2023年9月14日（周四）14:00-13:00

报告地点：海山楼A1101

校内联系人：杜磊 副教授

报告摘要：We consider the following matrix equation

AX + X⋆B = C,   (1)

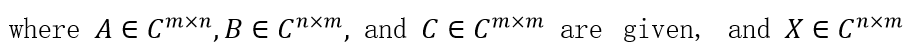
is to be determined. The operator (·)⋆ denotes the transpose (·)T or the conjugate transpose (·)H of a matrix. Equation (1) is called the ⋆-congruence Sylvester equation. The ⋆-congruence Sylvester equation appears in palindromic eigenvalue problems arising from some realistic applications such as the vibration analysis of fast trains, see e.g., [1].  In recent paper [2], when ⋆ = T and the given matrices are square (m = n), it was shown that the ⋆-congruence Sylvester equation is mathematically equivalent to the Lyapunov equation under certain conditions. The Lyapunov equation is widely known in control theory and has been much studied by many researchers. Therefore, the study [2] indicates that it can be possible to utilize the rich literature on the Lyapunov equation for the ⋆-congruence Sylvester equation (1). Indeed, it was shown that the direct method for the Lyapunov equation can be used to obtain a numerical solution of (1) with lower computational cost than the conventional method [4]. One of the important approaches in the previous study is to use an equivalent linear system that is obtained by vectorization. Oozawa et al. succeeded in reducing (1) to the Lyapunov equation by applying an appropriate linear operator to the linear system and returning it into a matrix.

The theoretical result was extended to the case where A and B are rectangular (m ̸= n). In this case, it was shown that (1) is equivalent to the generalized Sylvester equation [3]. However, when ⋆ = H, the same transformation cannot be applied to (1) because (1) is a nonlinear equation.

In this talk, we consider a linearization of (1) with ⋆ = H, and construct an appropriate operator to obtain an equivalent linear matrix equation. We show that (1) is equivalent to the generalized Sylvester equation under certain conditions, and introduce numerical solvers utilizing our results.

References

[1] D. Kressner et al., Numer. Algorithms, 51(2): 209–238, 2009.
[2] M. Oozawa et al., J. Comput. Appl. Math., 329: 51–56, 2018.
[3] Y. Satake et al., Appl. Math. Lett., 96: 7–13, 2019.
[4] F. D. Terán and F. M. Dopico, Electron. J. Linear Algebra, 22: 849–863, 2011.

报告人简介：张绍良，日本名古屋大学大学院工学研究科教授，名古屋大学中国交流中心主任。1983年吉林大学数学系本科毕业，1990年日本筑波大学博士毕业。曾在计算流体力学研究所（研究员），筑波大学（讲师），东京大学（副教授/教授）任职，2005年任现职。主要从事大型科学与工程计算的高速算法研究工作。张教授发展了Krylov子空间“乘积型迭代法”，在改良著名迭代法 Bi-CGSTAB的同时，借助Lanczos三阶递推公式，提出了解大型线性方程组的乘积迭代法的统一模型。由此统一模型，不仅可推导出著名的CGS法，Bi-CGSTAB法和Bi-CGSTAB2法，并且提出了一种新的方法：GPBi-CG法。计算结果表明GPBi-CG法是国际上现有的迭代法中精度最高，迭代速度最快，计算效率最有效的算法之一。张绍良教授曾/现任日本应用数理学会理事,日本应用数理学会副会长,日本应用数理学会会士, East Asia SIAM秘书长, 以及包括 International Journal of Numerical Analysis and Modeling，East Asian Journal on Applied Mathematics,Journal of Mathematical Research with Applications, Communications in Mathematical Research, CSIAM Transaction on Applied Mathematics, Transactions of the Japan Society for Industrial and Applied Mathematics, Bulletin of the Japan Society for Industrial and Applied Mathematics, 及Japan Journal of Industrial and Applied Mathematics等国际期刊编委。