报告题目： Bounded estimates for maximal operators associated to non-isotropic dilation of hypersurfaces in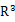

报告人：李文娟副教授 （西北工业大学）

报告时间：2020年7月3日 （星期五）下午3：00-4：00

腾讯会议 ID：385 770 797  密码：200703

报告摘要：The goal of this article is to establish $L^{p} \rightarrow L^{q}$ estimates for maximal functions associated with nonisotropic dilations $\delta_t(x)=(t^{a_1}x_1,t^{a_2}x_2,t^{a_3}x_3)$ of hypersurfaces $(x_{1}, x_{2},\Phi(x_1,x_2))$ in $\mathbb{R}^3$, where the Gaussian curvatures of the hypersurfaces are allowed to vanish. When $2 \alpha_{2} = \alpha_{3}$, this problem is reduced to  study of the $L^{p} \rightarrow L^{q}$ estimates for maximal functions along the curve $\gamma(x)=(x,x^2\phi(x))$ and associated dilations $(t,t^2)$. The corresponding maximal function shows features related to the Bourgain circular maximal function, whose $L^{p} \rightarrow L^{q}$ estimates have been considered by [Schlag, JAMS, 1997], [Schlag-Sogge, MRL, 1997] and [Lee, PAMS, 2003]. However, in the study of the maximal function related to the mentioned curve $\gamma(x)$ and associated dilations, we  get the $L^{p} \rightarrow L^{q}$ regularity properties for a family of corresponding Fourier integral operators which fail to satisfy the "cinematic curvature condition" uniformly, which means that classical local smoothing estimates could not be directly applied to our problem. What's more, the $L^{p} \rightarrow L^{q}$ estimates are also new for maximal functions associated with isotropic dilations of hypersurfaces $(x_{1}, x_{2},\Phi(x_1,x_2))$ mentioned before.  This is joint work with Dr. Huiju Wang.

报告人简介：李文娟, 西北工业大学数学与统计学院副教授。2018年入选陕西省高层次人才项目，2019年入选西北工业大学“翱翔新星计划项目”。2015年6月博士毕业于德国基尔大学，师从世界著名调和分析专家Detlef Mueller教授（1998年世界数学家大会45分钟报告者）。目前主持陕西省高层次人才计划项目、西北工业大学翱翔新星计划项目、中国博士后科学基金等项目。主要从事调和分析中算子有界估计等领域的研究，如多线性算子及其相关的极大算子和交换子、Fourier乘子算子、与超曲面相关的极大算子的有界估计等。已在J. Math. Pure.Appl.，J. Math. Anal. Appl. 等国际知名数学期刊上发表SCI论文十余篇。曾多次应邀访问美国伊利诺伊大学香槟分校、印第安纳大学伯明顿分校、德国基尔大学等。