学术报告
报告题目：An asymptotic distribution theory for Eulerian recurrences
报告人：黃顯貴 特聘研究员 台湾中央研究院统计科学研究所
报告时间：2017年11月17日（星期五）下午 13:30 -14:30
报告地点：创新园大厦 A1101
报告校内联系人：王毅 教授 联系电话：84708351-8128
报告摘要: We discuss linear recurrences of Eulerian type of the form
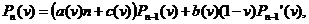
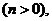with
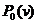given, where
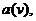
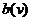and
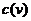are in most cases polynomials of low degree. We characterize the various limit laws of the coefficients of
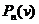for large
using the method of moments and analytic combinatorial tools under varying
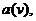
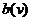and
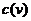. We apply our results to more than two hundreds of concrete examples that we collected from the literature and from Sloane's Online Encyclopedia of Integer Sequences. Not only most of the limit results are new, but they are unified in the same framework. The limit laws we worked out include normal, half-normal, Rayleigh, beta, Poisson,
negative binomial, Mittag-Leffler, Bernoulli, etc., showing the richness and diversity of such a simple recurrence scheme, as well as the generality and power of the approaches used.
报告人简介：黃顯貴，1994年12月在法国巴黎综合理工大学获博士学位，现为台湾中央研究院统计科学研究所，特聘研究员。研究兴趣为应用概率论、算法分析、渐近分析。连续三次获得国科会（现科技部）研究杰出奖；2003年，获德国洪堡基金会Bessel研究奖；2013年，获台法科技奖及教育部学术奖。
大连理工大学数学科学学院
2017年11月16日
