学术报告
报告题目:Some recent progresses in studies of the Tutte polynomial of a graph
报告人:叶永南 研究员 台北中央研究院数学所研究员
报告时间:2017年10月12日(星期四) 10:00 -11:00
报告地点:创新园大厦 A1101
报告校内联系人:王毅 教授 联系电话:84708351-8128
报告摘要: William Tutte is one of the founders of the modern graph. For every undirected graph, Tutte defineda polynomial
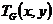 in two variables which plays an important role in graph theory. In this talk, we will introduce some recent progresses in studies of the Tutte polynomial of a graph. In Tutte’s original definitions, non-negative integers, called internal and external activities with respect to the arbitrary enumeration, are defined for each spanning tree, they serve as the indices of x and y in the product that is the corresponding term of Tutte polynomial. First, We will introduce the conceptions of σ-cut tail and σ-cycle tail of T, which are generalizations of the conceptions of internally and externally activities, repectively, where σ is a sequence on the edge set of G and T is a spanning tree of G. We will also discuss the conceptions of proper Tutte mapping and deletion-contraction mapping. In 2004, Postnikov and Shapiro introduced the concept of G-parking functions in the study of certain quotients of the polynomial ring. The Tutte polynomial of the graph G can be expressed in terms of statistics of G-parking functions. Let ∆ be a nonsingular M-matrix. We will introduce ∆-parking functions which is a generalization of G-parking functions. We will introduce the abelian sandpile model and ∆-recurrent configurations. There is a simple bijection between ∆-parking functions and ∆-recurrent configurations. We will discuss the geometry of sandpile model. Ingeneral, the Tutte polynomial encodes information about subgraphs of G. For example, for a connected graph G,
in two variables which plays an important role in graph theory. In this talk, we will introduce some recent progresses in studies of the Tutte polynomial of a graph. In Tutte’s original definitions, non-negative integers, called internal and external activities with respect to the arbitrary enumeration, are defined for each spanning tree, they serve as the indices of x and y in the product that is the corresponding term of Tutte polynomial. First, We will introduce the conceptions of σ-cut tail and σ-cycle tail of T, which are generalizations of the conceptions of internally and externally activities, repectively, where σ is a sequence on the edge set of G and T is a spanning tree of G. We will also discuss the conceptions of proper Tutte mapping and deletion-contraction mapping. In 2004, Postnikov and Shapiro introduced the concept of G-parking functions in the study of certain quotients of the polynomial ring. The Tutte polynomial of the graph G can be expressed in terms of statistics of G-parking functions. Let ∆ be a nonsingular M-matrix. We will introduce ∆-parking functions which is a generalization of G-parking functions. We will introduce the abelian sandpile model and ∆-recurrent configurations. There is a simple bijection between ∆-parking functions and ∆-recurrent configurations. We will discuss the geometry of sandpile model. Ingeneral, the Tutte polynomial encodes information about subgraphs of G. For example, for a connected graph G,
 is the number of spanning trees of G,
is the number of spanning trees of G,
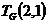 is the number of spanning forests of G,
is the number of spanning forests of G,
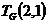 is the number of connected spanning subgraphs of G,
is the number of connected spanning subgraphs of G,
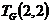 is the number of spanning subgraphs of G. At last, we will discuss combinatorial interpretations of
is the number of spanning subgraphs of G. At last, we will discuss combinatorial interpretations of
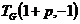 and
and
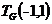 .
.
报告人简介:1978年毕业于台湾大学数学系,获得学士学位。于1983年与1985年在美国纽约州立大学水牛城分部数学系分别获得硕士与博士学位。1985年至1987年在加拿大魁北克大学蒙特娄分部信息与数学系作研究两年,1987年7月返台担任中央研究院数学所副研究员,1991年升等为研究员迄今;并先后于台师大信息系、台大信息系、交通大学数学系、成功大学数学系、彰师大数学系、台师大数学系、台大数学系担任兼任教授。1991年至1992年麻省理工学院数学所当访问学者一年;1995年夏天澳洲Monash大学经济所当访问学者;1999年夏天柏克莱大学统计所当访问学者一年。1992年及1994年获得国科会学术研究杰出奖(1次2年);2002年至2005年国科会学术一等奖。2009年至2012年国科会杰出计划研究奖;2011至2015年中央研究院学术杰出奖。
大连理工大学数学科学学院
2017年10月9日